Let's discover (variational) autoencoders and get going with a simple Tensorflow implementation.
Dans ce TP, vous allez implémenter un algorithme de compression x392 au moyen d'un réseau de neurones basique.
Si nous faisons abstraction du bias et des fonctions d'activation pour une seconde, les différentes couches d'un réseau de neurone ne sont rien de plus que des applications linéaires. Ces applications sont représentées par des tenseurs que nous pouvons considérer comme des changements de base.
Soit un tel réseau linéaire de \(N\) couches désignées \(L_i\) possédant un tenseur d'entrée \(X\) et une sortie \(Y\), nous avons donc $$ Y = \prod_{i=0}^N L_i X. $$
Ce réseau peut toujours être vu comme $$ Y =C T X,~\text{avec}~T=\prod_{i=1}^N L_i~\text{et}~C=L_0, $$ où \(T\) est un changement de base et \(C\) une application linéaire de classification.
Ce n'est pas étonant de voir apparaitre cette structure car ces changements de base visent, dans le cas d'un véritable réseau de classification (avec bias et fonctions d'activation), à rendre le problème linéairement séparable pour \(C\). L'idée derrière cette représentation reste en effet la même pour un réseau complet avec activation et bias. On doit cependant être plus prudent dans ce cas non linéaire et ne pas parler de changement de base mais plutôt de transformations. Les transformations ne sont plus représentables uniquement par une matrice, elles sont la combinaison d'une application linéaire, d'une fonction d'activation et d'un offset.
Une application très utile de telles transformations consiste à réduire le nombre de dimensions d'un ensemble de données. Réduire le nombre de dimensions est utile pour mieux observer les données, les caractériser ou les stocker. Nous retrouvons parmi ces méthodes l'ACP ou Analyse en Composantes Principales qui consiste à trouver la matrice de projection maximisant la projection de la variance sur les axes d'arrivée. On cherche à ce que chaque dimension de l'espace cible d'une ACP explique un pourcentage important de la variance du jeu de données. Bien souvent, deux dimensions sont visées afin de représenter les données sur un graphique.
Dans l'application qui nous concerne ici, nous allons mettre au point une transformation au principe analogue. Nous souhaitons représenter au mieux l'information présente dans un individu de notre ensemble de données tout en réduisant le nombre de dimensions investies dans sa description.
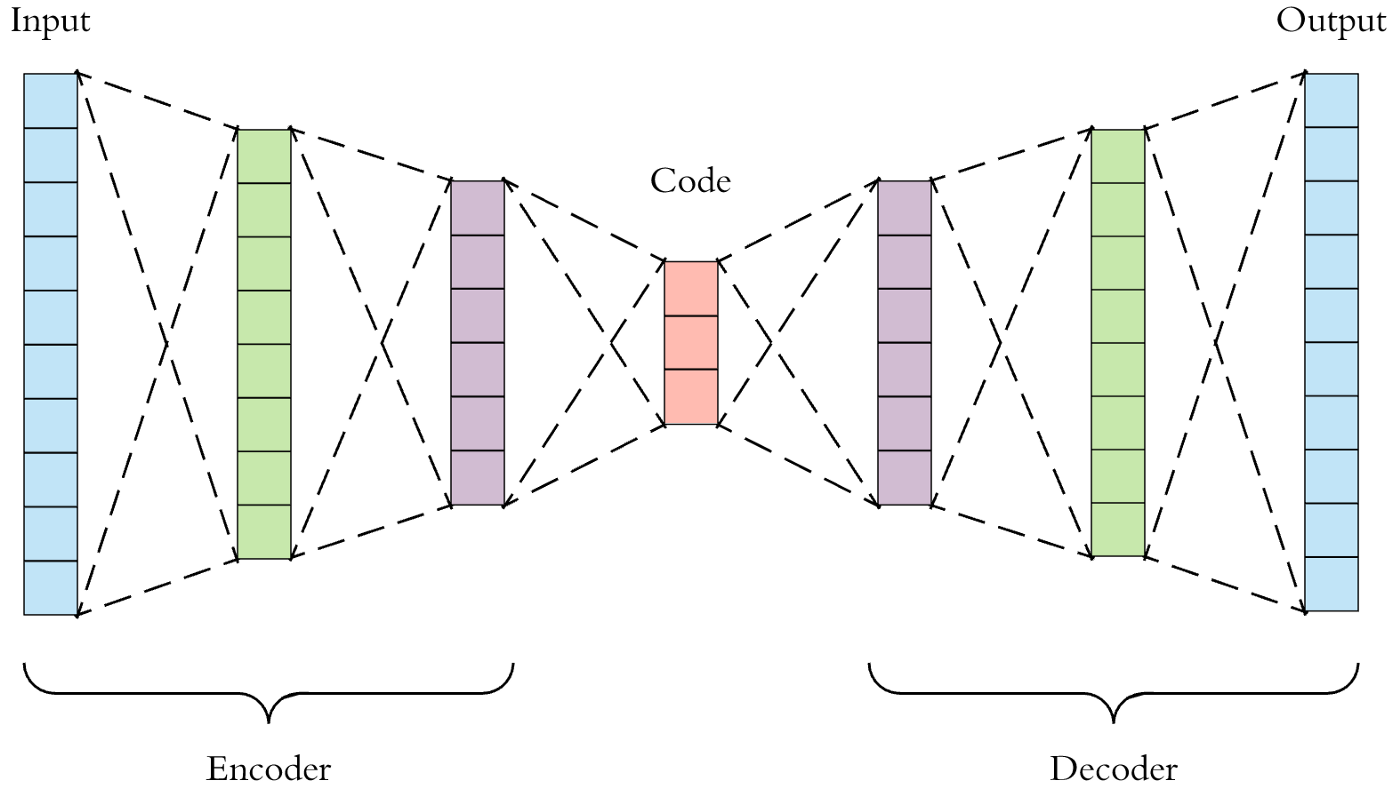
Le réseau de neurones présenté ci-dessous est une instance d'auto-ecodeur. Le goulot d'étranglement au centre est désigné espace latent et possède une faible dimension (ici 3). De part et d'autre du goulot, on retrouve l'encodeur, à gauche, qui va réduire la dimension de l'individu en vert et le décodeur qui va régénérer une sortie haute-dimension en rouge.
On remarque qu'on ne peut pas parler de transformation inverse pour le décodeur car une partie de l'information est perdue (voir aussi cours d'algèbre sur l'inversion d'applications). Nous sommes en effet face à une projection d'une part pour l'encodeur, non linéaire de surcroit. Le décodeur va permettre d'obtenir un résultat proche de l'inividu vert en combinant l'information commune à tous les individus, stockée dans le décodeur durant l'entrainement avec l'information à forte entropie présente dans le code en rouge. Pour formuler les choses autrement, l'information contenue dans le code est le distilat de ce qui distingue votre individu du reste de votre jeu de données. Cette dernière formulation est à mettre en parallèle avec le principe de l'ACP.

Pour commencer, il vous faudra rassembler les prérequis:
Pour télécharger le dataset, rien de plus simple: documentation
from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
Vous êtes libres d'employer l'architecture que vous souhaitez, pour démarrer je vous conseille la structure suivante. Il vous faudra réaliser un réseau en 5 couches:
Dans Keras, il est possible de composer un modèle à partir de sous-modèles séquentiels:
part1 = Sequential(Dense(32, input_shape=(10,)), Dense(8))
part2 = Sequential(Dense(16, input_shape=(8,)), Dense(64), Dense(2))
input = Input(shape=(10,))
network = part2(part1(input))
model = Model(input=input, output=network)
Cette représentation sera utile par la suite afin d'employer des portions du réseau séparément.
Toutes les couches sauf celle de sortie (sigmoid) emploient une fonction d'activation relu.
Afin de gérer les images 28x28, renseignez vous sur les couches Flatten et Reshape.
L'optimizer adam donnera les meilleurs résultats, une fonction d'aptitude adaptée est la binary\_crossentropy.
Enfin, n'oubliez pas de sauvegarder votre réseau après l'entrainement:
model.save("myautoencoder.h5")
Cette fonction sauvegarde à la fois la structure et les poids du réseau.
Maintenant que nous avons mis au point et entrainé un réseau auto-encodeur, nous allons l'utiliser et le visualiser.
Le modèle se charge simplement
from tensorflow.keras.models import load_model
from tensorflow.keras.utils import plot_model
model = load_model("myautoencoder.h5")
model.summary()
plot_model(model, to_file="model.png")
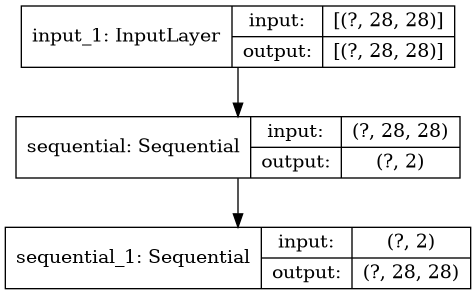
{ width=200px }
La seconde fonction permet de visualiser sous forme de texte la structure du réseau. La troisième produit une image png du réseau.
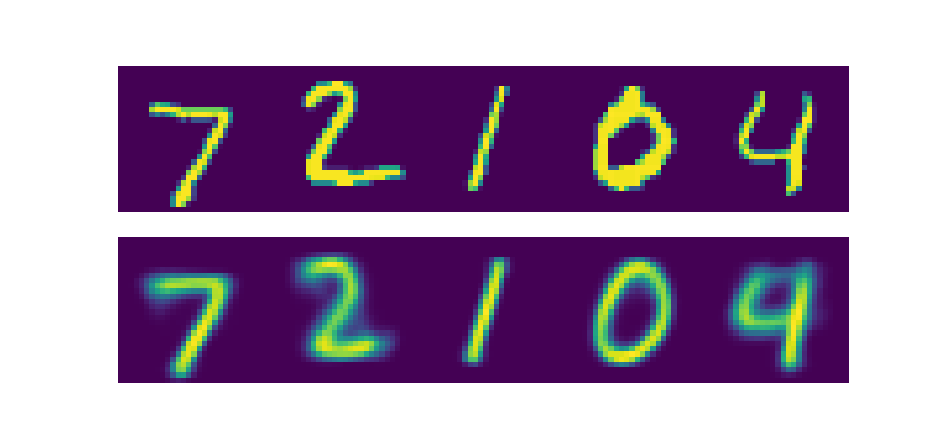
Dans cette partie finale du TP, vous allez manipuler l'encodeur et le décodeur séparément:
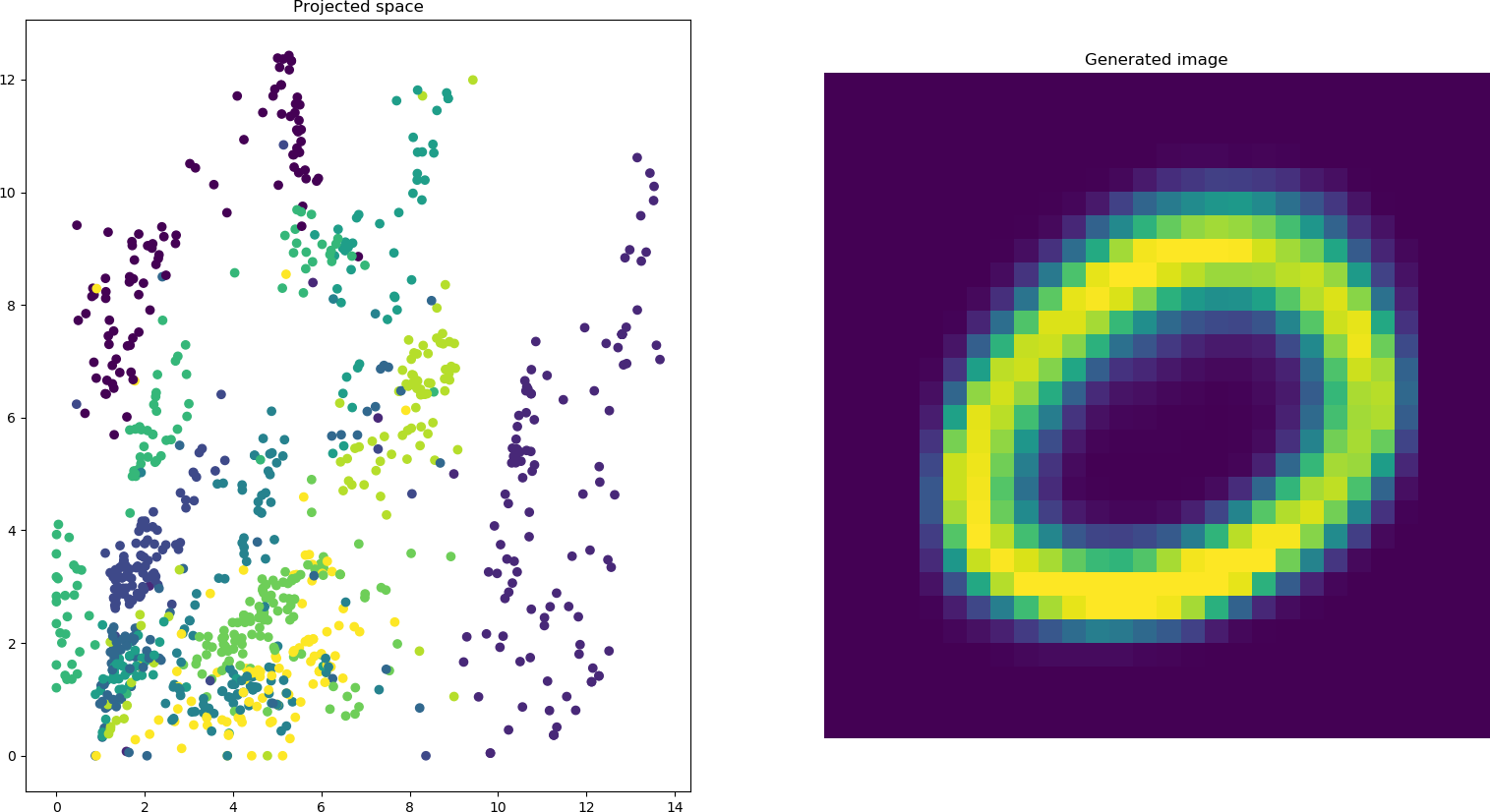
{width=400px}
home